布隆过滤器相关
如果想要快速判断一个元素是不是在一个集合里,可以怎么做?
一般想到的是用一种数据结构将所有元素保存起来,然后通过比较确定。
数组,链表,树等等数据结构都是这种思路.
但是随着集合中元素的增加,使用数组链表等结构,我们需要的存储空间越来越大,检索速度也越来越慢(O(n),O(logn))
。不过世界上还有一种叫作散列表(又叫哈希表,Hash table)的数据结构(有一个动态数组,+ 一个hash函数)。
但是有些时候我们只是需要知道某个元素是否在一个集合里面,其实并不需要存取这个元素本身,所以并不需要像hashMap或者hashSet
那样存下所有数据。这个时候就要引入布隆过滤器了。
什么是布隆过滤器
布隆过滤器(Bloom Filter)是1970年由布隆提出的,它实质上是一个很长的二进制向量和一系列随机映射函数 (Hash函数)。
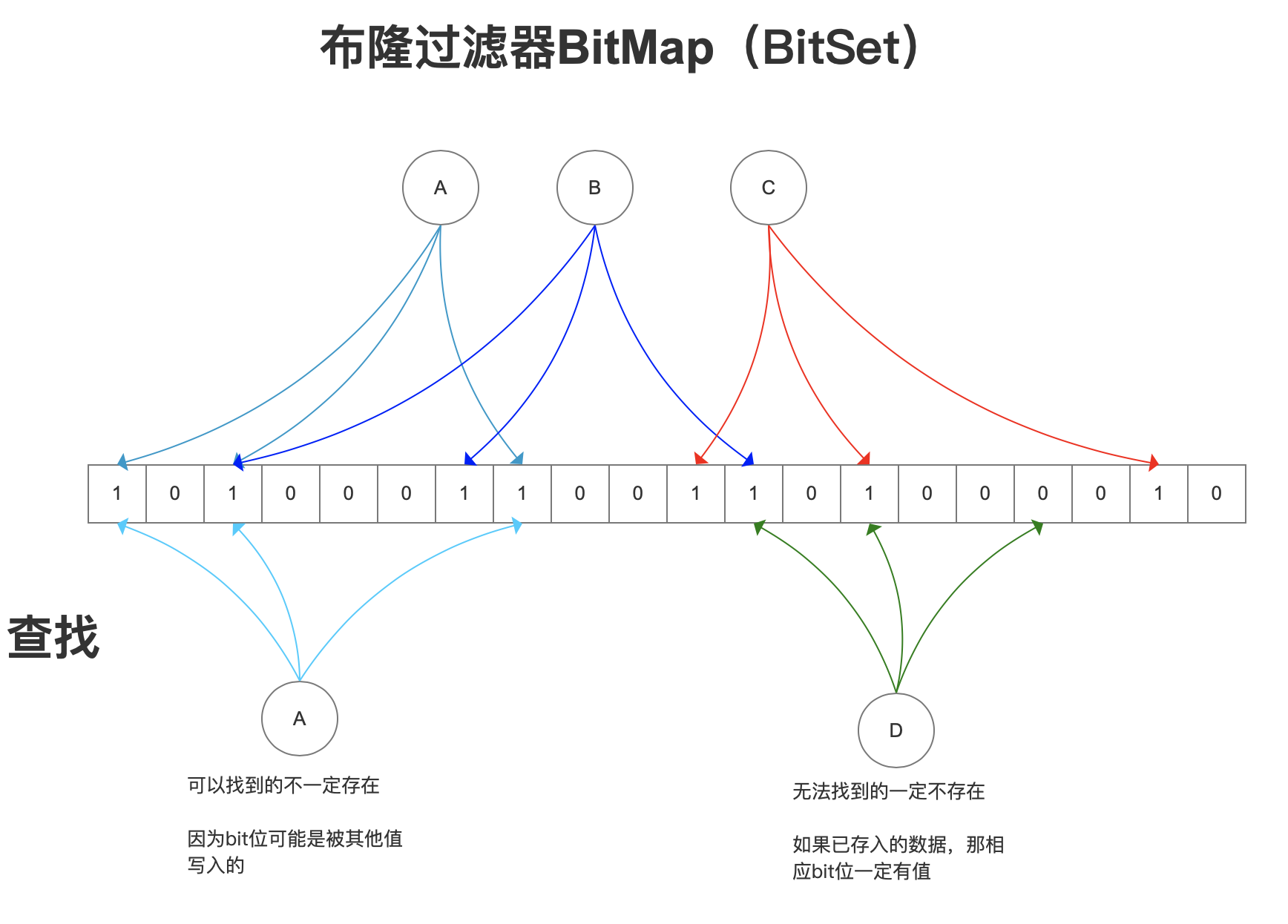
它用于判断这样的一个事情:某一个元素是否存在于一个集合里面。集合中的元素由哈希函数的映射规则,映射bitMap上的某一位;在bitMap上的每一位都是一个布尔类型的值,有两种状态0和1,0表示不存在于集合中,1表示存在于集合中,初始值都是0。这样相比较于使用数组、链表、哈希表等结构将集合中的元素本身存储下来,这样的做法,集合中的每一个元素只对应于bitMap的某几位,这样大大减少了存储的空间开销。
添加元素
布隆过滤器的两个主要的操作,一个是布隆过滤器初始化,往过滤器中添加元素;另一个是使用布隆过滤器查询一个元素。往布隆过滤器中添加元素往往发生在布隆过滤器的初始化环节。主要的步骤如下:
- 将要添加的元素进行哈希函数运算,得到该元素的哈希值;
- 将这个哈希值使用某种规则映射到bitMap数组上的某一位上(比如对数组的长度进行取模),如果这一位是0,则改为1;如果已经是1,则不用变;
- 一般布隆过滤器会有多个哈希函数,一个元素会被这多个哈希函数同时计算出多个哈希值,同时进行数组位置的映射,然后会将这多个映射位的状态值修改位1;
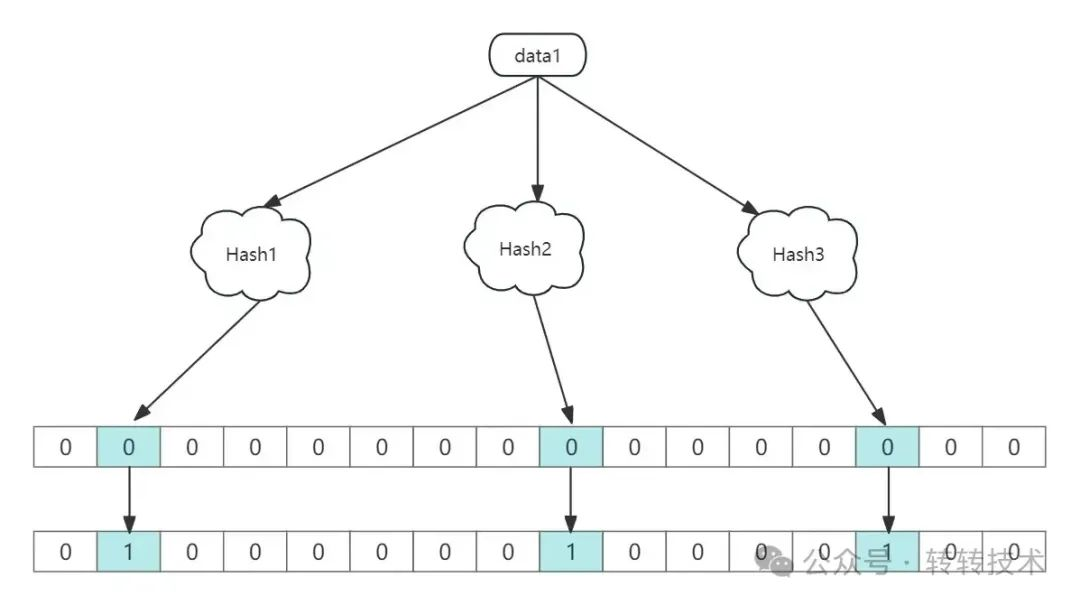
如上图所示:bitMap一开始全部是0,data1经过3个哈希函数的计算分别得到3个哈希值,将这3个哈希值同时映射到数组上,将对应数组位置上的值改为1,如此就完成了一个元素添加到布隆过滤器中的过程。
查询元素
布隆过滤器的另一个操作就是查询某一个元素是否在布隆过滤器中。主要的过程和添加元素非常类似:
- 将要查询的元素进行k个哈希函数的计算得到k个哈希值;
- 将这k个哈希值映射到数组上的k个位置;
- 检查这k个位置,如果有任何一个位置的值是0,则说明被查找的这个元素肯定不在布隆过滤器中;如果这k位全部都是1,说明被查找的元素可能在布隆过滤器中。
由上面的过程我们可以知道,布隆过滤器查询一个元素,可以给我们返回两种结论,这两种结论的情况不同:
- 当布隆过滤器返回元素不在集合中的时候,这个结论是靠谱的;
- 当布隆过滤器返回元素存在集合中的时候,这个结论是不靠谱的;
为什么会有这样的结论呢?
这就要讨论到哈希函数的特性了,由于哈希冲突的存在,以及底层bitMap数组长度的限制,肯定会出现这样的情况:两个不同的元素,经过同一个哈希函数计算后得到的哈希值一样(出现了哈希冲突),或者两个不同的哈希值,经过映射后,被映射在了数组的同一个位置。无论是上面的哪种情况,都会出现这样的现象,不同元素经过元素映射在数组的同一个位置,当查找的时候就无法确定这一位的状态被改成了1,究竟是哪一个元素添加进来的时候改的,不可避免的就会出现误判。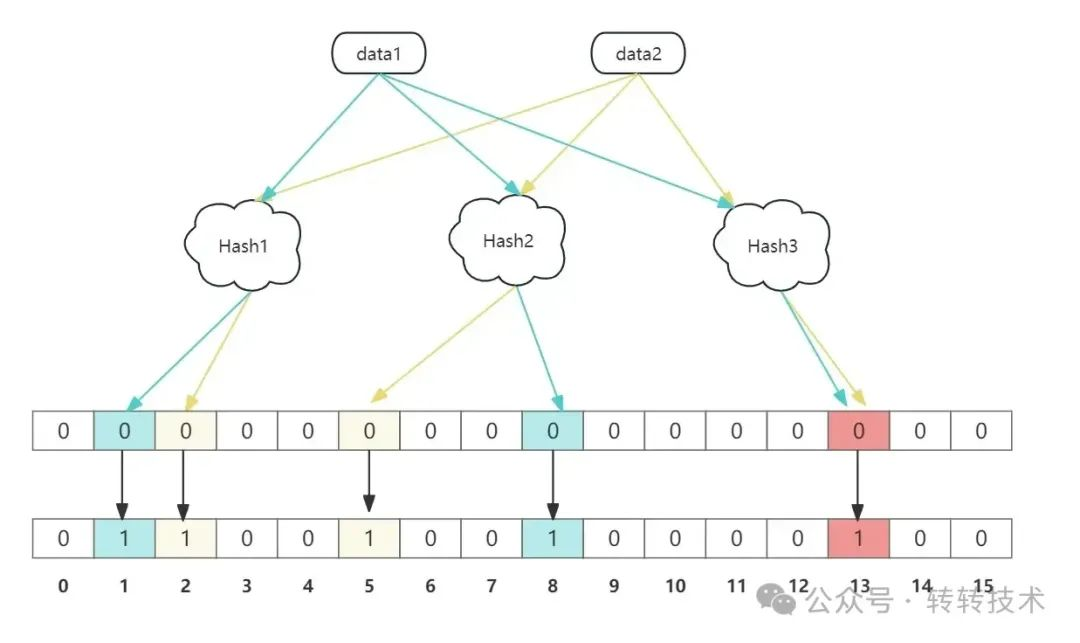
如上所示,data1和data2经过hash3函数映射后映射在了数组的同一个位置,假如现在要判断data2这个元素是否存在于布隆过滤器中,当判断到hash3这个位置的时候发现这一位是1,但是这意味有可能是data1添加进来的时候改成的1,虽然在上面的例子中仍然由hash1和hash2函数映射的位置可以判断(这就是为什么要有多个哈希函数的原因),但是其他的位置上面出现的1,同样也是有可能是冲突的结果,而并不是这个元素本身添加进来修改的,由此还是会不可避免的出现误判的问题。
误判率
由上面的内容可知,当我们要使用布隆过滤器判定元素存在于集合中的时候,是可能会存在误判的。误判的概率是多少呢?
参数:
m:布隆过滤器的bit长度。
n:插入过滤器的元素个数。
k:哈希函数的个数。
布隆过滤器的误判率计算公式:
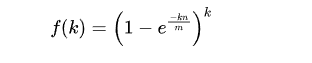
误判率的计算公式的推导过程如下:

在m和n一定,误判率尽量小的情况下,hash函数个数为:
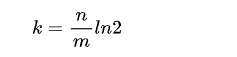
可以看到n和m一定的时候,可以算出k的最小值。
误判率和n确定的情况下,bit长度为:
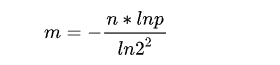
误判率和n成正相关,随者添加到布隆过滤器中的元素个数越来越多,误判率也会越来越大;和m成负相关,当数组的长度越大的时候,误判率会越小。
m,n,p,k之间的关系可以在这个网站上进行估计计算:https://hur.st/bloomfilter/
优点
布隆过滤器的最主要的优点就是极低的空间开销,集合中的一个元素,仅仅是映射成底层的几个比特位,这相比于其他的结构需要存储元素的所有信息而言,能节约非常多的内存开销,这意味这布隆过滤器的实现可以常驻在内存里面;时间复杂度也比较低,判断一个元素是否在布隆过滤器中的时间复杂度为O(
k)量级,k表示布隆过滤器内部的哈希函数的个数,一般这个值都不大。
缺点
但是布隆过滤器的缺点也比较明显。
- 首先就是它有一定的误判率,这个是由于哈希冲突所决定的,并且这个误判率会随着添加到布隆过滤器中的元素增加而升高;
- 另外一个比较明显的局限就是,布隆过滤器不支持删除元素操作。原因和上面的基本一样,如果先删除一个元素,将添加的过程逆向,就要将状态位1改为0,但是由于哈希冲突的存在,有可能会有别的元素同时也映射到这个位置,如果直接改为0,将意味着其他的元素可能会被误判。
布隆过滤器的应用
- 解决缓存穿透问题
什么是缓存穿透?
在一个使用了缓存的系统中,如果大量的查询数据库中本就不存在的数据,那么这些查询就会绕过缓存,直接打到数据库上面。应为一般来讲,数据库中不存在的数据,也不会在缓存中存在,所以如果大量请求查询数据库中本就不存在的数据,那么缓存层也就无法缓解了。
其实这样的问题还是有解决方法的:
- 做好接口的参数校验,对于一些恶意刷接口的请求进行拦截;
- 第一次查数据库的时候发现不存在,那么就将这个不存在的数据也缓存在缓存层里面,这样如果后续有查询重复查这个不存在的数据就能够在缓存层拦下来,从而不会对数据库造成太大的压力;
- 但是如果后面有源源不断的查询,查询之前没查过的,数据库中又不存在的数据的时候,上面的方法就无能为力了。
这个时候就要使用布隆过滤器来拦截了。通过在缓存层添加一个布隆过滤器,将数据库中明确存在的数据初始化到布隆过滤器中,对于后续的请求,查询缓存和数据库之前都先查找一下布隆过滤器,只要布隆过滤器返回不存在(上文提到,这个结论是靠谱的)那么这个元素一定不存在,可以直接返回空值,或者返回异常;如果布隆过滤器返回存在(这个结论不靠谱),我们就查询缓存,查询数据库,尽管布隆过滤器的这个结论是不靠谱的,可能会存在误报,即布隆过滤器返回了存在,但是实际上这个数据不存在,但是这个误报的概率足够小,就算让其请求进入到数据库查询,也不会对数据库造成什么压力。具体的流程如下:
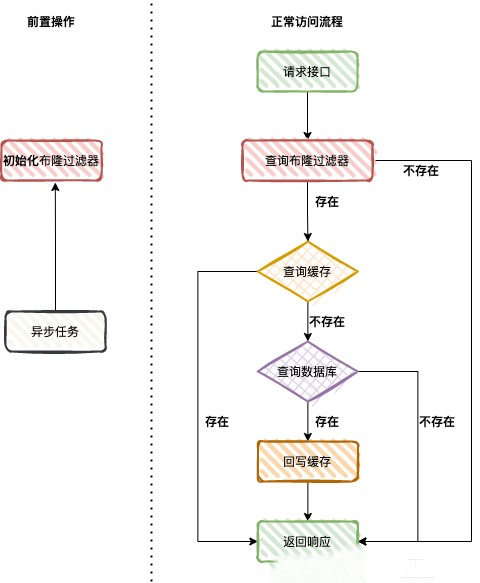
- 实现黑名单机制
对于接口安全方面的考虑,一个重要的手段是在接口上加上Ip白名单校验,或者Ip黑名单校验。一般接口业务是To B的话可以考虑进行白名单校验,这样接口的安全性更高;但是如果接口的业务是To C的话,就要考虑使用黑名单了。而布隆过滤器就可以实现,将一些恶意的ip地址添加到布隆过滤器中,每次都对请求Ip进行校验,如果不在布隆过滤器中,就通过,否则就拦截请求。
- 弱密码校验
在注册业务上,一般我们要求用户设置密码不能过于简单,比如像:12345678这样的密码,太过于简单,非常容易让人猜到,这样的密码就是我们说的弱密码。在注册接口中,我们都会判断一下用户设置的密码是否是常见的弱密码,如果是弱密码,则要求用户重新输入。对于这样的场景,也可以使用布隆过滤器来实现,将一些常见的弱密码初始化到布隆过滤器中,用户提交注册请求的时候判断其密码是否在布隆过滤器中,如果在的话就说明可能是弱密码,要求用户重新输入。
- 还有推荐系统,爬虫,甚至以太坊ETH的底层也使用了布隆过滤器来辅助实现一些功能…
布隆过滤器的实现
布隆过滤器的思想诞生了将近50年,已经有非常多的商业实现,这些实现都是经过了非常多的业务场景的考验的,常见的实现有Guava工具包的实现,Ridsson框架的实现,Redis官方的实现……
Guava工具包的实现
依赖
1 |
|
api
| 方法名 | 功能 | 参数 | 返回值 |
|---|---|---|---|
| put | 添加元素 | put(T object) | boolean |
| mightContain | 检查元素是否存在 | mightContain(T object) | boolean |
| copy | 根据此实例创建一个新的BloomFilte | copy() | BloomFilter |
| approximateElementCount | 已添加到Bloom过滤器的元素的数量 | approximateElementCount() | long |
| expectedFpp | 返回元素存在的错误概率 | expectedFpp() | double |
| isCompatible | 确定给定的Bloom筛选器是否与此Bloom筛选器兼容 | isCompatible(BloomFilterthat) | boolean |
| putAll | 通过执行的逐位OR将此Bloom过滤器与另一个Bloom过滤器组合 | putAll(BloomFilterthat) | void |
实例代码
1 |
|
Redisson框架的实现
依赖
1 |
|
api
| 方法名 | 功能 | 参数 | 返回值 |
|---|---|---|---|
| add | 添加元素 | add(T object) | boolean |
| contains | 检查元素是否存在 | contains(T object) | boolean |
| count | 已添加到Bloom过滤器的元素的数量 | count() | long |
| getExpectedInsertions | 返回的预期插入元素的个数 | getExpectedInsertions() | long |
| getFalseProbability | 返回元素存在的错误概率 | getFalseProbability() | double |
| getHashIterations | 返回每个元素使用的哈希迭代次数 | getHashIterations() | int |
| getSize | 返回此实例所需Redis内存的位数 | getSize() | long |
| tryInit | 初始化Bloom筛选器参数 | tryInit(long expectedInsertions, double falseProbability) | boolean |
| delete | 删除对象 | delete() | boolean |
实例代码
1 |
|
Redis官方插件的实现
依赖
1 |
|
api
| 命令 | 功能 | 参数 |
|---|---|---|
| BF.RESERVE | 创建一个大小为capacity,错误率为error_rate的空的Bloom | BF.RESERVE {key} {error_rate} {capacity} [EXPANSION {expansion}] [NONSCALING] |
| BF.ADD | 向key指定的Bloom中添加一个元素itom | BF.ADD {key} {item} |
| BF.MADD | 向key指定的Bloom中添加多个元案 | BF.MADD {key} {item …} |
| BF.INSERT | 向key指定的Bloom中添加多个元素,添加时可以指定大小和错误率,且可以控制在Bloom不存在的时候是否自动创建 | BF.INSERT {key} [CAPACITY {cap}] [ERROR {error}] [EXPANSION {expansion}] [NOCREATE] [NONSCALING] ITEMS {item …} |
| BF.EXISTS | 检查一个元秦是否可能存在于key指定的Bloom中 | BF.EXISTS {key} {item} |
| BF.MEXISTS | 同时检查多个元素是否可能存在于key指定的Bloom中 | BF.MEXISTS {key} {item …} |
| BF.SCANDUMP | 对Bloom进行增量持久化操作 | BF.SCANDUMP {key} {iter} |
| BF.LOADCHUNK | 加载SCANDUMP持久化的Bloom数据 | BF.LOADCHUNK {key} {iter} {data} |
| BF.INFO | 查询key指定的Bloom的信息 | BF.INFO {key} |
| BF.DEBUG | 查看BloomFilter的内部详细信息(如每层的元素个数,错误率等) | BF.DEBUG (key} |
实例代码
1 |
|
自己手写一个简单版的布隆过滤器
考虑的点:
选什么哈希函数?选计算性能高的,尽可能离散的。比如MurmurHash(Guava
实现的BloomFilter使用的是这个 https://github.com/aappleby/smhasher/blob/master/src/MurmurHash3.cpp)、KetamaHash等。到底进行几次hash映射k的值怎么选?二进制向量的长度设置为多少比较好?(有公式计算的)
布隆过滤器的局限和发展
其实布隆过滤器的局限性还是蛮大的,不支持删除就是其中比较突出的一个。
布隆过滤器诞生至今50多年了,产生了很多变种和改进型。
改进的方向:
- 更加高效的哈希函数(甚至完美哈希函数)
- 更加极致的空间利用率
- 支持删除
布隆过滤器的优化拓展: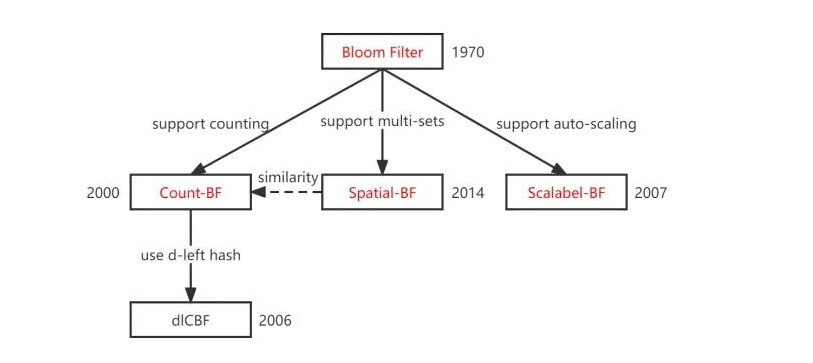
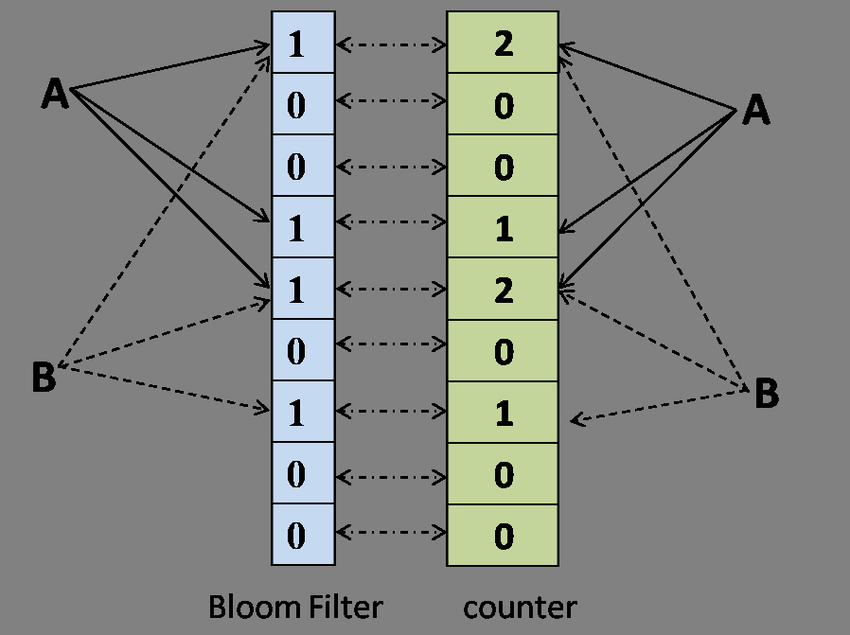
计数布隆过滤器
原理:
给定长度为 N*Mbits 的哈希空间。M 是用来存计数的位大小,比如当M取 4时,最大计数为 15,此时会溢出的概率已经足够小。
插入:选取 d 个哈希函数,每个哈希函数将给定的元素映射到[0,N-1]的一个位置上,并将该位对应的值+1。如果值大于 15,则取 15。
删除:选取 d 个哈希函数,每个哈希函数将给定的元素映射到[0,N-1]的一个位置上,并将该位对应的值-1。如果值小于 0,则取 0。
判断存在:和经典布隆过滤器相同。
代价呢?
使用了更多的空间,空间需求是经典布隆过滤器的M倍(m取决于底层存储的数组使用多少位来存储计数)
还是存在溢出的可能,一旦溢出,还是又造成误判的可能,或者一旦计数溢出了,误判的概率会变大。
删除一个元素之前,这个元素必须明确知道已经加入了过滤器中,不能删除未加入的元素。
布谷鸟过滤器
具有更好的空间利用率和更低的误判率,并且支持删除。但是复杂度太高。
参考:
https://www.cs.cmu.edu/~binfan/papers/conext14_cuckoofilter.pdf
http://www.linvon.cn/posts/cuckoo/
可扩展的布隆过滤器
因为大多数的时候对于要添加的元素个数是未知的,传统的布隆过滤器随者添加的元素越来越多,误判率也会越来越大,最后不得不重建。
但是Scalable Bloom Filter可以动态扩容。
注:Redis官方实现的布隆过滤器底层就是使用的可扩容的布隆过滤器
Redis官网对可扩展的布隆过滤器的介绍:
https://redis.io/blog/bloom-filter/
其他拓展的布隆过滤器
Ribbon Filter和Xor Filter:
阿里团队曾经将这个过滤器引入自己存储框架里面,并进行了测试,具体的详情参考:
https://developer.aliyun.com/article/980796